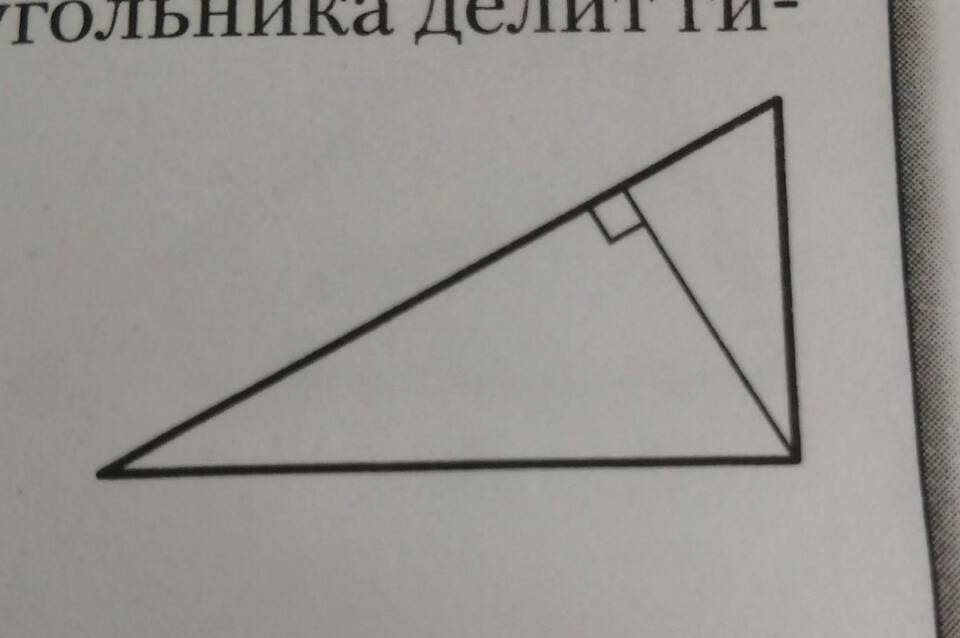
В прямоугольном треугольнике гипотенуза всегда меньше суммы двух катетов. Это фундаментальное свойство вытекает из геометрических закономерностей и теоремы Пифагора.
Содержание
В прямоугольном треугольнике гипотенуза всегда меньше суммы двух катетов. Это фундаментальное свойство вытекает из геометрических закономерностей и теоремы Пифагора.
1. Математическое обоснование
| Элемент | Обозначение | Соотношение |
| Катет 1 | a | c < a + b |
| Катет 2 | b | |
| Гипотенуза | c |
2. Доказательство через теорему Пифагора
- По теореме: c² = a² + b²
- Сравним (a + b)² и c²:
- (a + b)² = a² + 2ab + b²
- c² = a² + b²
- Так как 2ab > 0, то (a + b)² > c²
- Следовательно: a + b > c
3. Геометрическая интерпретация
Три варианта соотношений сторон:
- Прямая линия (вырожденный треугольник): c = a + b
- Обычный треугольник: c < a + b
- Невозможный случай: c > a + b (нарушение неравенства треугольника)
4. Практические примеры
| Катет a | Катет b | Гипотенуза c | Сумма a + b |
| 3 | 4 | 5 | 7 |
| 5 | 12 | 13 | 17 |
| 7 | 24 | 25 | 31 |
5. Следствия из этого свойства
- Кратчайший путь между точками - прямая (гипотенуза)
- Обоснование неравенства треугольника
- Применение в оптимизационных задачах
- Использование в строительстве и проектировании
Важные выводы:
- Гипотенуза - самая длинная сторона, но меньше суммы катетов
- Разница между суммой катетов и гипотенузой увеличивается с ростом углов
- В равнобедренном прямоугольном треугольнике c = a√2 < 2a
Соотношение длин гипотенузы и суммы катетов демонстрирует фундаментальное свойство прямоугольных треугольников, имеющее многочисленные практические применения в математике и смежных науках.
