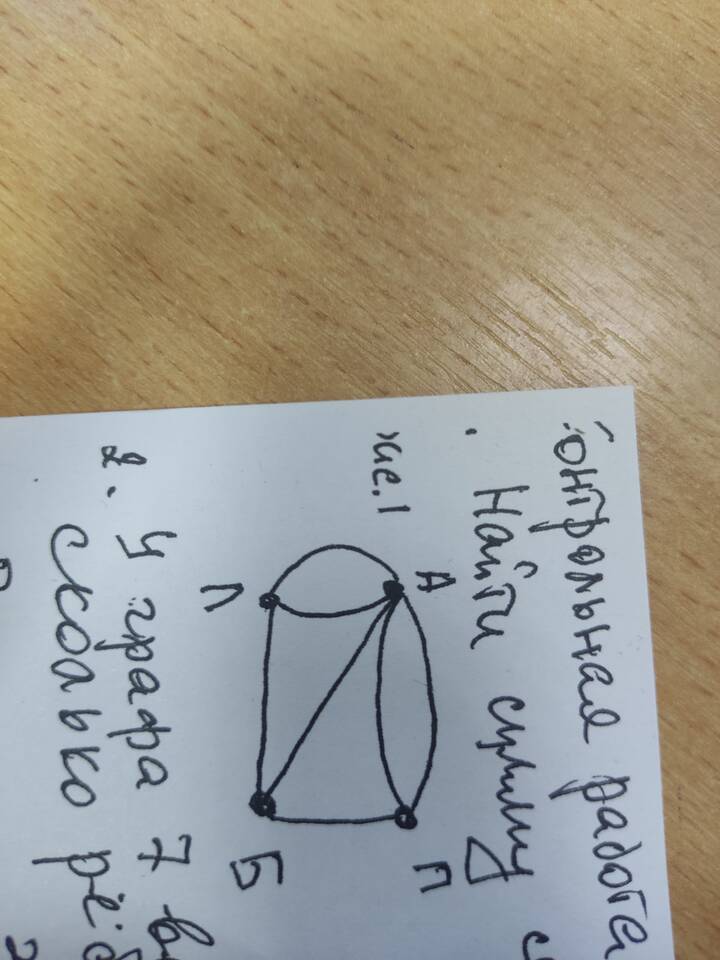
В теории графов степень вершины - это количество рёбер, инцидентных данной вершине. Сумма степеней всех вершин графа имеет фундаментальное значение и подчиняется строгим математическим закономерностям.
Содержание
Основная теорема о сумме степеней
Для любого графа (ориентированного или неориентированного) сумма степеней всех его вершин равна удвоенному количеству рёбер:
- Для неориентированного графа: ∑deg(v) = 2|E|
- Для ориентированного графа: ∑deg⁺(v) + ∑deg⁻(v) = |E|
где |E| - количество рёбер в графе, deg(v) - степень вершины v, deg⁺(v) - полустепень исхода, deg⁻(v) - полустепень захода.
Следствия из теоремы
Лемма о рукопожатиях
В любом неориентированном графе количество вершин с нечётной степенью всегда чётно.
Оценка количества рёбер
Зная сумму степеней вершин, можно определить количество рёбер: |E| = (∑deg(v))/2
Примеры расчётов
| Тип графа | Степени вершин | Сумма степеней | Количество рёбер |
| Треугольник | 2, 2, 2 | 6 | 3 |
| Звезда с 4 лучами | 4, 1, 1, 1, 1 | 8 | 4 |
| Полный граф K₄ | 3, 3, 3, 3 | 12 | 6 |
Применение в задачах
Проверка существования графа
Последовательность натуральных чисел может быть последовательностью степеней вершин некоторого графа тогда и только тогда, когда сумма этих чисел чётна.
Построение графов
- Определите желаемые степени вершин
- Проверьте, что их сумма чётна
- Постройте граф, удовлетворяющий условиям
Особые случаи
- Для регулярных графов (где все степени равны) сумма степеней равна n×k, где n - число вершин, k - степень каждой вершины
- В деревьях сумма степеней равна 2(n-1), где n - количество вершин
- Для эйлеровых графов все степени вершин чётны
Знание свойств суммы степеней вершин является мощным инструментом при анализе графов и решении задач теории графов. Это фундаментальное свойство находит применение в компьютерных науках, химии, социологии и других областях.